一定要收藏！高中数学常用二级结论50条！帮你节约做题时间！

结论1：在椭圆

上不与坐标轴平行的弦的斜率与该弦中点和坐标原点连线的斜率之积为定值

（注：若椭圆焦点在y轴上时，即

，则定值为

）。

证明：设原点为O，A（

），B（

）是椭圆上的任意不同的两点，P（

）是弦AB中点。

，

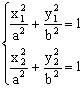
由以上几式可得：

。可转化为

，即

。

结论2：双曲线

上不与坐标轴平行的弦的斜率与该弦中点和坐标原点连线的斜率之积为定值

（注：若双曲线为焦点在y轴上的形式，则定值为

）。

证明：设原点为O，A（

），B（

）是双曲线上的任意两个不同的点，P（

）是弦AB的中点。

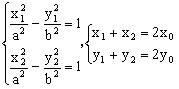
由以上几式可得：

。可转化为

，即

。

结论3：抛物线

上不与坐标轴平行的弦的斜率与该弦中点和坐标原点连线的斜率之积为

（

为弦中点的横坐标）。

证明：设原点为O，A（

），B（

）为

上任意两个不同的点，P（

）为弦AB中点。

可得：

两边同除以（

）得：

即得：

。

解决圆锥曲线中有关弦的斜率与中点坐标问题时，用“设而不求，代点作差”解题较麻烦，运用上述结论解题，简捷快速。

例1、求中心在原点O，一焦点为（0，

），截直线

所得弦的中点横坐标为

的椭圆的方程。

解：设

与椭圆交于A（

），B（

），AB中点为P（

），

。P（

）在

上得

，由上述结论知

，而

。

所以

。由题意知

。

解得

，故椭圆方程为

。

例2、求与椭圆

相交于A、B两点并且线段AB中点为（1，1）的直线方程。

解：设原点为O，A（

），B（

），AB中点坐标为P（1，1）。

由上述结论知

，而

，所以

。

所求直线方程为

。

例3、已知双曲线

，求以A（2，1）为中点的弦的方程。

解：设原点为O，M（

），N（

），则所求直线斜率

，

，

。

由结论知

，而

，所以

。

所求直线方程为

，即

。

例4、双曲线中心在原点，且一个焦点为F（

，0），直线

与双曲线交于M、N两点，MN中点P的横坐标为

，求双曲线方程。

解：设原点为O，因为一个焦点为F（

，0），所以可设双曲线方程为

（a>b，b>0）。

MN中点P

在

上，得

。

的斜率为1，而

，所以

。

又因为

，所以，

。

则双曲线方程为

。

例5、直线

与抛物线

交于A、B两点，AB中点横坐标为2，则k的值为（）

A. －1

B. 2

C. －1或2

D. 以上都不是

解：设原点为O，AB中点为P（

），则

。M（

）在

－2上，则

。而

，即

，解得

（不符合题意舍去）或

。故选B。

铁律1：

函数或方程或不等式的题目，先直接思考后建立三者的联系。首先考虑定义域，其次使用“三合一定理”。

铁律2：

函数或方程或不等式的题目，先直接思考后建立三者的联系。首先考虑定义域，其次使用“三合一定理”。

铁律3

面对含有参数的初等函数来说，在研究的时候应该抓住参数没有影响到的不变的性质。如所过的定点，二次函数的对称轴或是……

铁律4：

选择与填空中出现不等式的题目，优选特殊值法。

铁律5

求参数的取值范围，应该建立关于参数的等式或是不等式，用函数的定义域或是值域或是解不等式完成，在对式子变形的过程中，优先选择分离参数的方法。

铁律6

恒成立问题或是它的反面，可以转化为最值问题，注意二次函数的应用，灵活使用闭区间上的最值，分类讨论的思想，分类讨论应该不重复不遗漏。

铁律7

圆锥曲线的题目优先选择它们的定义完成，直线与圆锥曲线相交问题，若与弦的中点有关，选择设而不求点差法，与弦的中点无关，选择韦达定理公式法；使用韦达定理必须先考虑是否为二次及根的判别式。

铁律8

求曲线方程的题目，如果知道曲线的形状，则可选择待定系数法，如果不知道曲线的形状，则所用的步骤为建系、设点、列式、化简（注意去掉不符合条件的特殊点）。

铁律9

求椭圆或是双曲线的离心率，建立关于a、b、c之间的关系等式即可。

铁律10

三角函数求周期、单调区间或是最值，优先考虑化为一次同角弦函数，然后使用辅助角公式解答；解三角形的题目，重视内角和定理的使用；与向量联系的题目，注意向量角的范围。

铁律11

数列的题目与和有关，优选和通公式，优选作差的方法；注意归纳、猜想之后证明；猜想的方向是两种特殊数列；解答的时候注意使用通项公式及前n项和公式，体会方程的思想。

铁律12

立体几何第一问如果是为建系服务的，一定用传统做法完成，如果不是，可以从第一问开始就建系完成；注意向量角与线线角、线面角、面面角都不相同，熟练掌握 它们之间的三角函数值的转化；锥体体积的计算注意系数1/3，而三角形面积的计算注意系数1/2；与球有关的题目也不得不防，注意连接“心心距”创造直角 三角形解题。

铁律13

导数的题目常规的一般不难，但要注意解题的层次与步骤，如果要用构造函数证明不等式，可从已知或是前问中找到突破口，必要时应该放弃；重视几何意义的应用，注意点是否在曲线上。

铁律14

导数的题目常规的一般不难，但要注意解题的层次与步骤，如果要用构造函数证明不等式，可从已知或是前问中找到突破口，必要时应该放弃；重视几何意义的应用，注意点是否在曲线上。

铁律15

遇到复杂的式子可以用换元法，使用换元法必须注意新元的取值范围，有勾股定理型的已知，可使用三角换元来完成。

铁律16

注意概率分布中的二项分布，二项式定理中的通项公式的使用与赋值的方法，排列组合中的枚举法，全称与特称命题的否定写法，取值范或是不等式的解的端点能否取到需单独验证，用点斜式或斜截式方程的时候考虑斜率是否存在等。

铁律17

绝对值问题优先选择去绝对值，去绝对值优先选择使用定义。

铁律18

与平移有关的，注意口诀“左加右减，上加下减”只用于函数，沿向量平移一定要使用平移公式完成。

铁律19

关于中心对称问题，只需使用中点坐标公式就可以，关于轴对称问题，注意两个等式的运用：一是垂直，一是中点在对称轴上。