
2017年高考虽然已经落下帷幕,但讨论高考的声音依然热烈。因为高考每年都有,接下去高二升高三的“准高三”学子们,要开始准备2018年高考。
俗话说知己知彼百战不殆,“准高三”学子们可以认真好好的研究一下2017高考,这样对于自己明年参加高考,可以起到一定启示和帮助。如高考数学填空题是一份高考数学试卷重要题型,可以说,一名考生只要做好填空题,做对填空题,那么你的高考数学分数就不会低了!
因此,我们今天就来简单讲讲高考数学填空题,希望对大家学习能起到帮助。

填空题是大家最熟悉的题型之一,也是高考数学必考题型,同时分值也较高。填空题只要求填写结果,每道题填对了得满分,填错了得零分,同时很多考生在填空题上失分一般比选择题和解答题严重,如何解好高考数学填空题,大家一定要加以重视。
填空题和选择题一样都属于客观题,主要考查考生对数学知识概念的理解、解决问题能力和推理论证能力等等,同时要考虑后面大题的时间,这就要求我们考生在解决填空题的时候要尽可能在短时间内作答。如一些高水平的考生一般每道题都在1~3分钟内就可以完成,这些都是需要较高的解答策略和方法。
纵观近几年高考数学填空题,一般可以分为这么几类:完形填空题、多选填空题、条件与结论开放的填空题等等。
典型例题1:

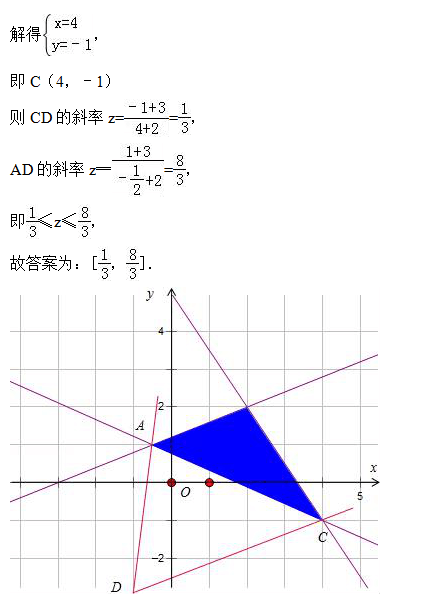
考点分析:
简单线性规划的应用.
解题反思:
作出不等式组对应的平面区域,利用z的几何意义,结合数形结合即可得到结论。
根据填空题的答案回答形式,我们可以把填空题分成两种类型:
第一种是定量型
要求学生填写数值、数集或数量关系,如:方程的解、不等式的解集、函数的定义域、值域、最大值或最小值、线段长度、角度大小、概率等等。由于填空题和选择题相比,缺少选择支的信息,所以以往高考题中多数是以定量型问题出现。
典型例题2:
已知a,b,c分别是锐角△ABC的三个内角A,B,C的对边,a=1,b=2cosC,sinCcosA﹣sin(π/4﹣B)sin(π/4+B)=0,则△ABC的内角B的大小为 .
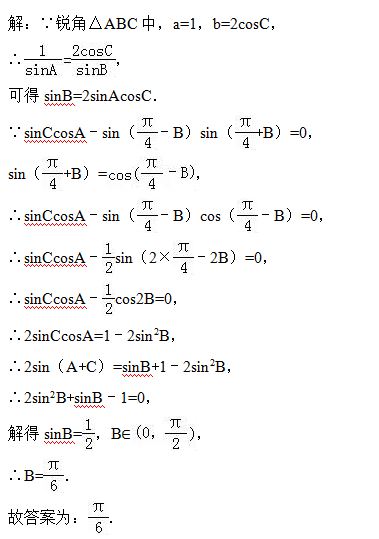
考点分析:
余弦定理;两角和与差的正弦函数;正弦定理.
题干分析:
a=1,b=2cosC,利用正弦定理可得:sinB=2sinAcosC.
由sinCcosA﹣sin(π/4﹣B)cos(π/4﹣B)=0,利用诱导公式可得:
sinCcosA﹣1/2sin(2×π/4﹣2B)=0,利用倍角公式可得:
2sinCcosA=1﹣2sin2B,联立化简即可得出.
第二种是定性型填空题
要求填写的是具有某种性质的对象或者填写给定的数学对象的某种性质,如:给定二次曲线的准线方程、焦点坐标、离心率等等,在高考中还可能会出现更多的定性型的填空形式,如:对命题的叙述、算法中的伪代码或运行条件、归纳类比推理中的结论、乃至对一些实际应用问题结果的阐述等。

要想拿到填空题全部分数,那么我们在做题的时候就要做到正确、快速、合理、简捷等等。同时要快速抓住解题要领,运算要快,同时不可操之过急,审题要仔细,不能粗心大意,答案要回答全,力戒小题大作。
典型例题3:
若数列{an}满足a2﹣a1>a3﹣a2>a4﹣a3>…>an+1﹣an>…,则称数列{an}为“差递减”数列,若数列{an}是“差递减”数列,且其通项an与其前n项和Sn(n∈N*)满足2Sn=3an+2λ﹣1(n∈N*),则实数λ的取值范围是 .
解:∵2Sn=3an+2λ﹣1(n∈N*),
∴n=1时,2a1=3a1+2λ﹣1,
解得a1=1﹣2λ.
n≥2时,2an=3an﹣3an﹣1,
化为an=3an﹣1.
同理可得:a2=3(1﹣2λ),a3=9(1﹣2λ),a4=27(1﹣2λ).
∴a2﹣a1=2(1﹣2λ),a3﹣a2=6(1﹣2λ),a4﹣a3=18(1﹣2λ),
∵a2﹣a1>a3﹣a2>a4﹣a3>…,
∴2(1﹣2λ)>6(1﹣2λ)>18(1﹣2λ),
解得:λ>1/2.
则实数λ的取值范围是λ>1/2.
故答案为:λ>1/2.
考点分析:
数列的函数特性.
题干分析:
2Sn=3an+2λ﹣1(n∈N*),n=1时,2a1=3a1+2λ﹣1,解得a1=1﹣2λ.n≥2时,可得:an=3an﹣1.利用a2﹣a1>a3﹣a2>a4﹣a3>…,即可得出。
同时大家还可以记住以下这几种高考数学填空题的解法:
1、特殊化法
当填空题的结论唯一或其值为定值时,我们只须把题中的参变量用特殊值(或特殊函数、特殊角、特殊数列、图形特殊位置、特殊点、特殊方程、特殊模型等)代替之,即可得到结论。但要注意所选取的 值要符合条件且计算起来较简单。
2、直接推演法
直接从题设条件出发,利用定义、性质、定理、公式等,经过变形、推理、计算、判断得到结论的方法,称之为直接求解法。它是解填空题的常用的基本方法。使用直接法解填空题,要善于透过现象抓本质,自觉地、有意识地采取灵活、简捷的变换。

3、构造法
此法有些与特殊值解填空题有相似之处,它主要通过观察、联想、分析、转化等把未知的变为已知的或基本题型。可以构造特例、构造函数、构造图形、构造模型等,让解题更为巧妙。
4、数形结合法
根据题设条件的几何意义,画出问题的辅助图形,借助图形的直观性,通过对图形的分析判断,得出正确结论。
为了能很好考查考生的数学能力,每年高考数学填空题都会有一定变化,所以我们一定要不断提高自己解题水平,关注高考数学题型变化。
