高考数学冲刺再提分
数学作为高考三大主科之一,其重要程度不言而喻。最后两个月,若能掌握正确的方法就有希望再提高10到20分?这里有各个分数段的冲刺攻略,还有考点分析,为了你的数学,一起来看看吧~
各分数段提分技巧

一、110分~130分
基本的成绩是110分左右,若是想进一步想提高到130分左右,应该专项突破。
选填题:
难度应该控制在中档偏上,如高考题中最后两个选择题的难度。主要集中在函数、导函数、圆锥曲线、数列。有时间可以扩散的章节:均值不等式、向量、解斜三角形、立体几何、三角函数等等。
圆锥曲线大题和导函数:
难度控制在高考的难度。一般的圆锥曲线难在计算过程中对表达式的处理上:怎么处理这样的式子,怎么处理?需要在做题之后多总结,多去揣摩。导函数的难度就比较大了,需要练习的时候多做总结,找出所练习这些题目之中有什么共同的地方,不同的地方,怎么去思考,以后遇到这样的题是否可以用这样的方法和解题的思路,这个过程需要反复的揣摩。
二、90分~110分
如果你的成绩目前是90左右,估计你分值应该是这么来的:选择题对7-8个,填空题对3-4个,前四个大题三角函数、概率比较简单,容易拿分,数列和立体几何难度较大一点,估计能拿第一个问,这样就是36分的样子,后面的20、21题会有一点得分,这样差不多就是90分。
专项突破——前四个大题突破:
三角函数与解斜三角形
基本知识点准备:诱导角公式、同角三角函数的基本关系、二倍角公式、正余弦定理、三角函数的基本公式等等。
基本方法准备:一般的,三角恒等变换常见的思路是:求三角函数的最值、单调性、图像、对称性、周期是都需要用辅助角公式,在之前要降次。
解斜三角形的解题方法:
对于“边”的一次式(分式、等式)----首先想到正弦定理
已知△ABC的三个内角A,B,C所对的边分别为a,b,c,asinAsinB+bcos2A=a,则等于()
题型练习:挑选一些难度和高考难度相当,题量在10到12个就可以了。一定要总结,结合解题方法总结。
接下来就是概率、立体几何、数列方法同上。在平时综合试卷测试的基础上观察哪一个板块、哪一个知识点出了问题,就针对这个板块,这个知识点进行专项的复习,这样选填题能拿高分。
至少一周有一次数学综合考试,难度和高考的难度持平,发现问题就复习,这样慢慢的弥补你所有的漏洞。
三、60分~90分
如果你的成绩只有60分左右,估计你的分数这样的:选择题对5-6个,填空题对1-2个,前四个大题中,概率估计能拿分,其余的可以拿第一个小问,差不多是60分样子。
只有60分的成绩说明基础比较薄弱,要想在眼前的时间里面再把高一到高三的所有课程再复习一遍基本上是不可能了,那怎么办呢?
分版块复习:
三角函数和解斜三角形:
知识点由学生自行浏览复习,针对部分知识点下的题型有问题要放慢复习的进度,比如:诱导角公式有困难,可以针对这个知识点进行迅速的补习突破。这个期间需要做一定量的题型,其目的就是在短时间里快速的达到灵活运用知识点(毕竟高考主要就是考察知识点的灵活运用)。
概率:
有针对性的知识点和考点进行复习(这个章节的考点角明显):三个抽样、茎叶图、直方图求中位数、平均数、众数的求法,概率中的古典概型、几何概型。这个是文科主要考察得几个考点。理科在这个基础上有随机事件分布、相互独立事件、平均值,方差等等。有针对性的练习和突破可以拿满分的。
立体几何:
三视图、体积、表面积(三个可以一起复习)点线面的位置关系(线面、面面平行,线面、面面垂直可以分开复习)。主要讲解方法,比如:线面平行可以通过面面平行证明。文科主要考察这些。理科考察二面角,可以学习一下求二面角的方法,不过很多同学都会选择用建系的方法来做。除此之外就是练习,要一定量的题型,多做总结。
数列:
等差、等比数列知识点,以及知识点下的题型练习、以及通项公式的求法和前n项和的求法,再这样的基础上加以练习即可,做练习的时候一定要和做讲的知识点、方法相结合,多总结。
以上四个板块复习之后起目的就是要做好高考前面四个大题以及之前的选填题。
接下来就是针对选填题的章节复习:
函数、向量、不等式、直线方程、圆的方程、圆锥曲线、导函数。在复习的时候主要是踩点(考点),比如不等式,选填题一般容易一个基本的不等式、线性规划的考察,线性规划主要考察那些题型就可以了。
在复习圆锥曲线的导函数的时候尽可能的能做高考的第一个问,求圆锥曲线的轨迹方程,导函数的最值、极值、单调性、尤其是分类讨论的单调性。
近年数学考点分析
冲刺阶段,要想效率最大化,让数学再提10~20分,就要从考点分析看起,掌握并预测考点,从这方面集中突破,把力都使在刀刃上。
下图为2008年到2016年高考全国乙(文科)客观题考点分布情况(其中1—12为选择题,13—16为填空题,这里把选择11—12及填空15—16作为压轴题标红)
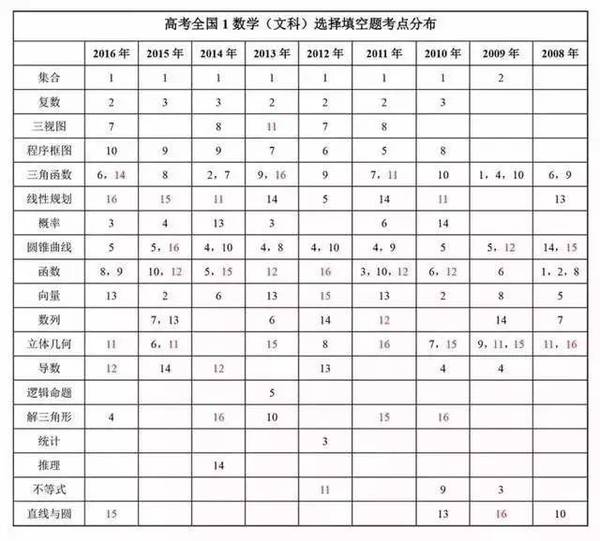
下图为2004年到2016年高考全国乙卷(理科)选择题、填空题考点分布情况(其中1-12为选择题,13-16为填空题,这里把选择11-12及填空15-16作为压轴题):
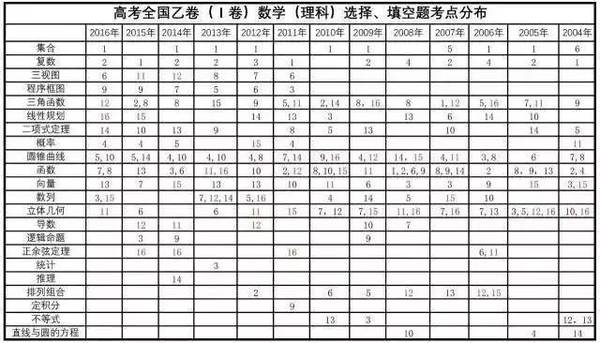
下图为2010-2016年高考数学全国卷(文科)解答题考点分布情况:
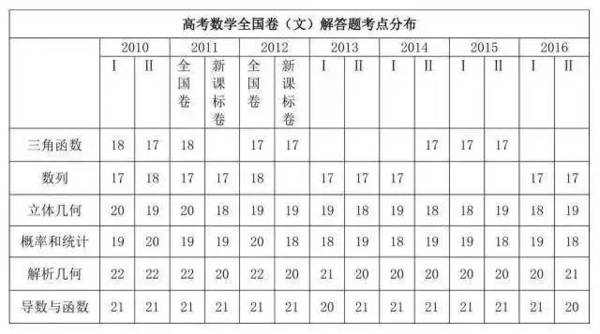
下图为2007年到2016年高考全国乙卷(理科)解答题考点分布情况(圆锥曲线和导数题为压轴题):
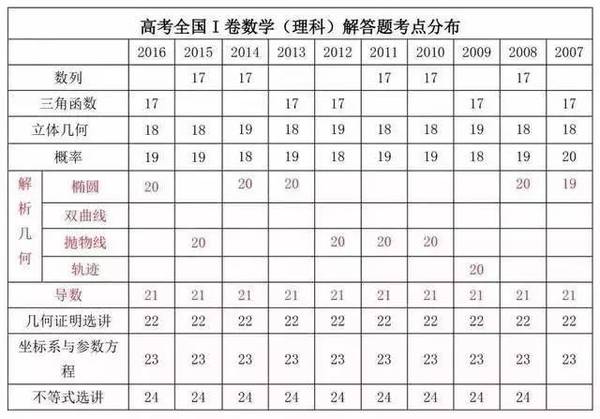
2017高考数学核心考点预测

一、选择与填空
1.数学集合的基本运算(含新定集合中的运算,强调集合中元素的互异性);
2.常用逻辑用语(充要条件,全称量词与存在量词的判定);
3.数学函数的概念与性质(奇偶性、对称性、单调性、周期性、值域最大值最小值);
4.幂、指、对函数式运算及图像和性质
5.函数的零点、函数与方程的迁移变化(通常用反客为主法及数形结合思想);
6.空间体的三视图及其还原图的表面积和体积;
7.空间中点、线、面之间的位置关系、空间角的计算、球与多面体外接或内切相关问题;
8.数学直线的斜率、倾斜角的确定;直线与圆的位置关系,点线距离公式的应用;
9.数学算法初步(认知框图及其功能,根据所给信息,几何数列相关知识处理问题);
10.古典概型,几何概型理科:排列与组合、二项式定理、正态分布、统计案例、回归直线方程、独立性检验;文科:总体估计、茎叶图、频率分布直方图;
11.三角恒等变形(切化弦、升降幂、辅助角公式);三角求值、三角函数图像与性质;
12.数学向量数量积、坐标运算、向量的几何意义的应用;
13.正余弦定理应用及解三角形;
14.等差、等比数列的性质应用、能应用简单的地推公式求其通项、求项数、求和;
15.线性规划的应用;会求目标函数;
16.圆锥曲线的性质应用(特别是会求离心率);
17.数学导数的几何意义及运算、定积分简单求法
18.复数的概念、四则运算及几何意义;
19.抽象函数的识别与应用;
二、解答题
1.向量与三角交汇问题,解三角形,正余弦定理的实际应用;
2.(高考文科数学)概率与统计(概率与统计相结合型)
(高考理科数学)离散型随机变量的概率分布列及其数字特征;
3.数学立体几何
①证线面平行垂直;面与面平行垂直
②求空间中角(理科特别是二面角的求法)
③求距离(理科:动态性)空间体体积;
第20题:解析几何(注重思维能力与技巧,减少计算量)
①求曲线轨迹方程(用定义或待定系数法)
②直线与圆锥曲线的关系(灵活运用点差法和弦长公式)
③求定点、定值、最值,求参数取值的问题;
4.数学函数与导数的综合应用
这是一道典型应用知识网络的交汇点设计的试题,是考查考生高考数学解题能力和数学素质为目标的压轴题。
主要考查:分类讨论思想;化归、转化、迁移思想;整体代换、分与合思想
一般设计三问:
①求待定系数,利用求导讨论确定函数的单调性;
②求参变数取值或函数的最值;
③探究性问题或证不等式恒成立问题。
三、高考数学三选一:
(1)数学几何证明主要考查三角形相似,圆的切割线定理,证明成比例,求角度,求长度;利用射影定理解决圆中计算和证明问题是历年高考题的热点;
(2)数学坐标系与参数方程,主要抓两点:参数方程、极坐标方程互化为普通方程;有参数、极坐标方程求解曲线的基本量。这类题,思路清晰,难度不大,抓基础,不做难题。
(3)数学不等式选讲:绝对值不等式与函数结合型。设计上为:①解含有参变数关于x的不等式;②求解不等式恒成立时参变数的取值;③证明不等式(利用均值定理、放缩法等)。
