【例题】(天津卷)
函数f(x)的定义域为开区间(a,b),导函数f’(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点几个?
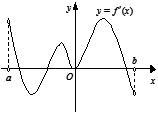
解析思路:这个题目考察的就是,函数的导数和函数图象性质的对应关系,大家要熟悉导数大于0,小于0对于原函数的意义,而且还有二次求导的问题,二次求导后现根据导数判断一次求导的单调性,一定要注意看值域,因为一次求导跟原函数有关的一定是大于0小于0的情况,而不是单调的情况,所以把自己的做题思路先理清楚。所以本题答案显而易见应该是1个极小值点。

技巧破解+例题拆解4:对于导数与其他知识结合。
处理方法还是基本的思路先求导去判断导数零点的情况,然后分类讨论的标准也许从它的下一步开始进行,比如字母参数从零点开始讨论,字母参数从题目给定的范围开始讨论,分几种情况,分类讨论。但是尤其是注意,看清楚下题中的三角函数是否是参数还是常数。
【例题】

解题思路:
第一小题明显直接求解就好,第二小题首先根据导数情况求导找到极小值点,然后与不等式结合求解不等式的解集,第三部,恒成立问题还是要转化为最值问题,但是要讨论区间范围到底是在小于0的范围还是在另一个范围,所以首先理清楚思路,再去求解会相对简单一些。




总结
导数的题目虽然变化多,但是思路对于分类讨论的点还是比较固定的,只是讨论的情况有时候因题而异,所以大家在总结时多找这些规律,把导数的题目拿到手呢!
